[A* Algorithm] A* 알고리즘의 개념과 구현
게임 속 적들은 모두 스스로 움직인다.
즉, 본인의 위치부터 플레이어의 위치까지 스스로 경로를 파악하고 움직이고 있는 것이다.
그것도 무작위로 오는게 아닌, 최단 경로를 스스로 파악하고 걸어온다.
그럼 컴퓨터는 이 최단 경로를 어떻게 아는걸까?
최단 경로를 얻는 알고리즘엔 BFS나 다익스트라(Dijkstra) 알고리즘들도 매우 좋은 답이지만,
오늘 소개할 A* 알고리즘은 게임 엔진 속 최단 경로 탐색에 좋은 답이 될 것이다.
A* 알고리즘의 출발
A* search algorithm - Wikipedia
From Wikipedia, the free encyclopedia Algorithm used for pathfinding and graph traversal A* (pronounced "A-star") is a graph traversal and pathfinding algorithm that is used in many fields of computer science due to its completeness, optimality, and optima
en.wikipedia.org
A* 알고리즘은 1968년, Peter Hart, Nils Nilsson, Bertram Raphael이라는 세 연구자가 발표한 논문에서 처음 등장했다.
이 알고리즘은 단순한 최단 경로 탐색이 아니라,
효율성과 정확성을 동시에 추구하는 스마트한 탐색법을 목표로 만들어졌다.
기본적으로는 다익스트라 알고리즘의 아이디어를 기반으로 하고 있지만,
여기에 휴리스틱(Heuristic)이라는 개념을 더해서 성능을 비약적으로 높인 방식이라고 볼 수 있다.
BFS나 다익스트라는 모든 경로에 대한 최단 경로를 전부 파악해버리지만,
A* 알고리즘은 최대한 목적지까지 도달하는 스마트한 방법을 파악하기 때문에 성능적으로 매우 좋다.
개요 : A* 알고리즘이란?
A* 알고리즘은 목적지까지 가는 가장 빠른(또는 비용이 가장 적은) 경로를 찾는 알고리즘이다.
그렇다면 비용이라는 것을 알아야 하는데, 비용은 어떻게 알 수 있을까?
기본적인 흐름은 이렇다.
- 지금까지 온 거리(G)와
- 앞으로 남은 거리(H)를 합산해서
- 총 예상 비용(F = G + H)이 가장 낮은 후보부터 탐색해 나간다.
한마디로, 지금까지 온 거리도 중요하게 보지만 앞으로 얼마나 더 가야 하는지도 같이 고려하는 방식이다.
F, G, H에 대해서 조금 더 자세히 알아보자.
F = G + H
G는 시작점에서 현재 위치까지 실제로 이동한 누적 거리다.
예를 들어 한 칸 이동할 때 비용이 1이라면, 시작점에서 5칸 이동한 위치의 G값은 5가 된다.
정말 현재 좌표까지 몇 걸음동안 걸어왔냐는 수치이기 때문에 이해하기 매우 쉬울 것이다.
최단 경로를 찾는 것이기 때문이 적을 수록 좋다.
H는 현재 위치에서 목적지까지의 예상 거리를 의미한다.
이 값은 실제 거리와는 다를 수 있지만, 대략적인 감을 잡기 위한 추정값이다.
가장 많이 쓰이는 방식은 맨해튼 거리(Manhattan Distance) 또는 유클리드 거리(Euclidean Distance)이다.
맨해튼 거리는 목적지까지 남은 가로 거리 + 세로 거리이고,
유클리드 거리는 목적지까지의 대각선을 포함한 최소 직선 거리이다.
이 역시 최단 경로를 찾는 것이기 때문이 적을 수록 좋다.
F는 최종 비용이며, G + H를 통해 산출된다.
이 값이 작을수록 더 가능성 있는 경로라고 판단된다.
A*는 이 F값이 가장 낮은 후보를 우선적으로 탐색한다.
알고리즘의 동작 순서
A* 알고리즘의 동작 순서를 알기 위해선 몇 가지 개념을 알아야 한다.
우선 첫 번째로 오픈 리스트이다. 오픈 리스트는 출발한 주인공 기준에서 인지하게 된 길 후보들이다.
미로를 풀어낼 우리들은 미로에 어떤 길들이 있는지 전혀 모르기 때문에, 출발하는 플레이어 기준에서 갈 수 있다고 판단되는 모든 길들은 우선 오픈 리스트에 담아두게 된다.
두 번째로 클로즈 리스트이다. 클로즈 리스트는 탐색 완료한, 방문한 길들이다.
이미 한 번 방문한 길은 다시 방문하지 않아야 하기 때문에 꼭 필요한 리스트이다.
A* 알고리즘의 순서는 아래와 같다.
- 시작 지점을 오픈 리스트에 추가한다.
- 오픈 리스트에서 F값이 가장 작은 노드를 꺼낸다.
- 이 노드를 클로즈 리스트에 넣는다.
- 꺼낸 노드의 인접한 노드들을 확인한다.
- 벽이거나 이미 닫힌 리스트에 있는 경우는 제외
- 아직 발견하지 않았거나, 더 좋은 경로가 있다면 오픈 리스트에 넣는다.
- 목적지에 도착할 때까지 위 과정을 반복한다.
굉장히 쉬워보이지만, 놀랍게도 이 과정을 반복하는 것 만으로 반드시 최적해를 보장하며 목적지에 도달한다.
그렇다면 여기서 비용적으로 비싸보이는 것이 무엇이 있을까 살펴보니,
바로 수많은 오픈 리스트들의 값들 중 F값이 가장 작은 노드를 꺼내는 것이 문제처럼 보인다.
정렬되지 않은 리스트에서 max값이나 min값을 찾으려면 O(n)의 시간복잡도가 소요되므로,
우리는 리스트에 특정 값을 넣을 때 항상 정렬을 유지하며 이진 탐색을 해야 한다.
그렇다고 list에 값을 넣을 때마다 계속 sorting 알고리즘을 실행했다간 오히려 더 비용이 비싸질 수도 있는데,
이렇게 최대, 최솟값을 지속적으로 추가하고 꺼내야하는 상황에서 역시 가장 좋은 자료구조라면 바로 우선순위 큐이다.
우선순위 큐
오픈 리스트에서 "F값이 가장 낮은 노드"를 빠르게 꺼내려면, 단순한 리스트보다는 우선순위 큐를 사용하는 게 좋다.
이 큐는 F값을 기준으로 자동 정렬되기 때문에, 효율적으로 다음 탐색 후보를 관리할 수 있다.
우선순위 큐는 언제나 최대, 최솟값을 빠르게 꺼내고, 새로운 값을 빠르게 추가할 수 있는 자료구조인데,
이는 이진 탐색 트리, 혹은 힙 구조로 이루어진 자료구조이다.

일반 FIFO 구조의 큐와는 다르게 우선순위 큐는 항상 포화 이진 트리의 모양을 유지하며,
최대 힙이냐, 최소 힙이냐에 따라 루트 노드에 항상 최댓값 혹은 최솟값을 유지한다.
더더욱 쉽게 풀어보자!
그럼에도 A* 알고리즘이 어려울 수 있는 독자들을 위해,
정말 쉽게 하나씩 풀어보도록 하겠다.

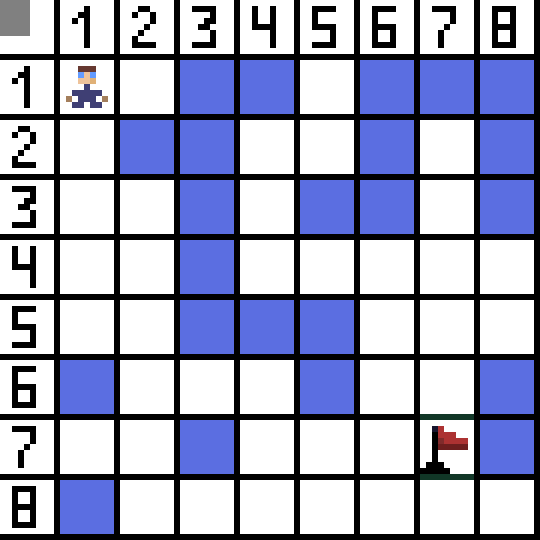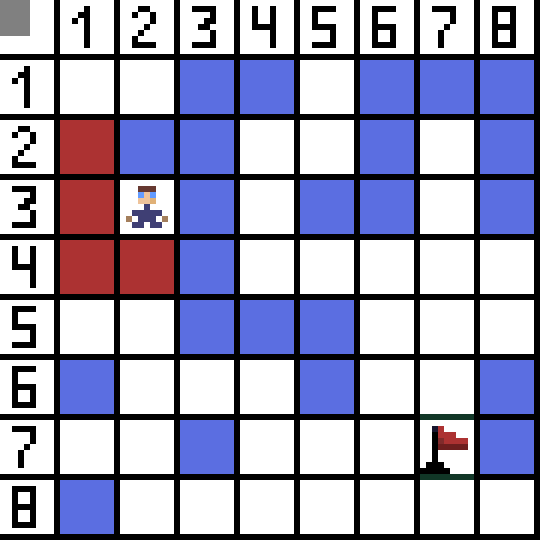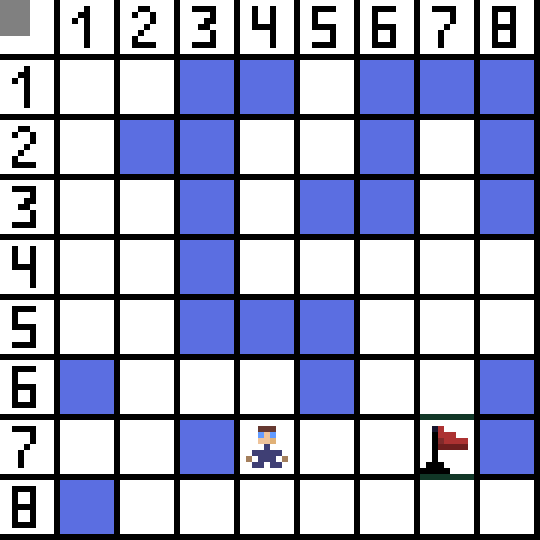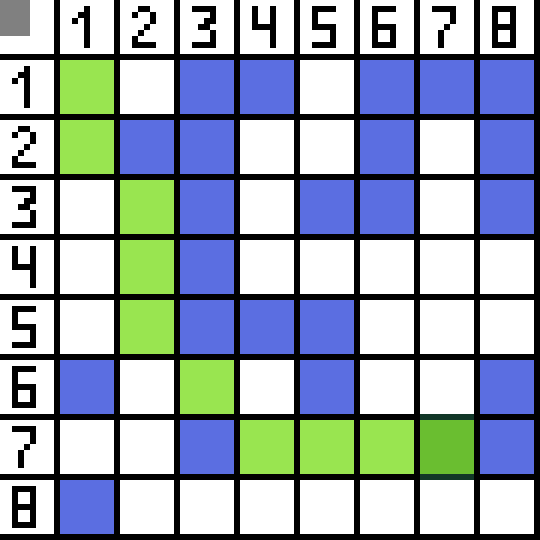
위와 같은 미로가 있다고 쳐보자.
플레이어 기준에서 오른쪽으로 가는 길은 실제로 목적지까진 도달하지 못하는 막다른 길이다.
그럼에도 불구하고 A* 알고리즘은 우선 오른쪽 길로 가게 된다.
왜냐하면, 그 길이 F값이 가장 작은, 현재 기준에서 가장 현명해보이는 길이기 때문이다.

그러나 막상 가고보니 더 이상 현재 기준에선 갈 수 있는 곳이 없다.
왼쪽은 이미 방문했던 (클로즈 리스트) 길이고, 그 외 방향은 모두 벽이기 때문이다.
이 때 시점에서 오픈 리스트에서 가장 F값이 적은 값은, 1번으로 적어둔 길일 것이다.

그 순서대로 가다보면, 최대한 효율적인 길을 따라가다보니까 누가봐도 목적지까지 가지 않는 비효율적인 길은 우선 오픈 리스트에 넣어 고려는 해두지만 결국 가보지도 않게 된다.
목적지까지 가는 더 효율적으로 보이는 길을 우선 시도해보다가, 결국 목적지에 도착하기 때문에 나머지 후보는 고려할 조차 없기 때문이다.
만약 BFS나 다익스트라였다면, 저 가보지도 않았던 길들 역시 출발점으로부터 얼만큼의 최소 비용이 들었는지 모두 계산했을 것이다. 그러나 A* 알고리즘은 이를 고려하지 않았고, 그만큼 시간적으로 이점을 보게 된다.
C# 에서의 A* 구현 코드
void AStar()
{
int[] deltaY = new int[] { -1, 0, 1, 0 };
int[] deltaX = new int[] { 0, -1, 0, 1 };
int[] cost = new int[] { 1, 1, 1, 1 };
// 점수 매기기
// F = G + H
// F : 최종 점수, 작을 수록 좋으며 경로에 따라 달라짐
// G : 시작점에서 해당 좌표까지 이동하는데 드는 비용, 작을 수록 좋으며 경로에 따라 달라짐
// H : 휴리스틱. 목적지에서 얼마나 가까운지 직선거리로 계산, 작을 수록 좋으며 고정됨
// (y, x) 좌표에 이미 방문했는지 여부 (방문 = closed 상태)
bool[,] closed = new bool[_board.Size, _board.Size];
// (y, x) 좌표에 가는 길을 한 번이라도 발견했는지
// 발견 X => MaxValue
// 발견 O => F = G + H
int[,] open = new int[_board.Size, _board.Size];
for (int y = 0; y < _board.Size; y++)
for (int x = 0; x < _board.Size; x++)
open[y, x] = Int32.MaxValue;
// 오픈 리스트에 있는 정보들 중에서 가장 좋은 후보를 빨리 뽑는 도구
PriorityQueue<PQNode> pq = new PriorityQueue<PQNode>();
// 시작점 발견 (예약 진행)
open[PosY, PosX] = Math.Abs(_board.DestY - PosY) + Math.Abs(_board.DestX - PosX);
pq.Push(new PQNode() { F = Math.Abs(_board.DestY - PosY) + Math.Abs(_board.DestX - PosX), G = 0, Y = PosY, X = PosX });
while (pq.Count > 0)
{
// 제일 좋은 후보를 찾는다
PQNode node = pq.Pop();
// 동일한 좌표를 여러 경로를 찾아서, 더 빠른 경로로 인해 이미 방문된 경우면 스킵
if (closed[node.Y, node.X])
continue;
// 방문
closed[node.Y, node.X] = true;
// 목적지에 도착했다면 알고리즘 종료
if (node.Y == _board.DestY && node.X == _board.DestX)
break;
// 상하좌우 이동할 수 있는 좌표인지 확인 후 예약한다
for (int i = 0; i < deltaY.Length; i++)
{
int nextY = node.Y + deltaY[i];
int nextX = node.X + deltaX[i];
// 유효범위 벗어나면 스킵
if (nextY < 0 || nextY >= _board.Size || nextX < 0 || nextX >= _board.Size)
continue;
// 벽이라면 스킵
if (_board.Tile[nextY, nextX] == Board.TileType.Wall)
continue;
// 이미 방문한 곳이면 스킵
if (closed[nextY, nextX])
continue;
// 비용 계산
int g = node.G + cost[i];
int h = Math.Abs(_board.DestY - nextY) + Math.Abs(_board.DestX - nextX);
// 다른 경로에서 더 빠른 길을 찾았다면 스킵
if (open[nextY, nextX] < g + h)
continue;
// 지금까지 찾은 케이스중에선 가장 빠른 값이니 예약 진행
open[nextY, nextX] = g + h;
pq.Push(new PQNode() { F = g + h, G = g, Y = nextY, X = nextX });
}
}
}
위 코드는 SideWinder 알고리즘으로 랜덤 생성된 미로를 탈출하는 A* 알고리즘 코드이다.
실제로 미로를 푸는 것을 디스플레이할 땐 지나갔던 경로에 어디서부터 왔는지 parent를 담고, 목적지로부터 parent를 역순으로 따져본다면 최단 경로가 디스플레이될 것이다.
A* 알고리즘에 대해 알아봤는데, 고급 알고리즘이다보니 꽤 어려운 얘기가 많이 들어갔다.
이를 이해하기 위해선 우선순위 큐를 알아야 하고, 그걸 알기 위해선 힙과 트리를 알아야 하며, 이를 알기 위해선 또 그래프 이론의 선수 지식이 필요하다.
하나씩 차근차근 자료구조와 알고리즘을 공부하다보면, 분명 A* 알고리즘이 어느샌가 쉽다고 느껴질 것이다.