9375. 패션왕 신해빈
이번엔 엄청 어려운 문제는 아니지만, 앞으로 풀어갈 조합론 문제들에 대해 접근하는 방식의 토대를 심어주는 중요한 문제를 들고 왔다.
이 유형은 매우 유명해서 프로그래머스의 의상이라는 거의 동일한 문제로도 존재한다.
나의 풀이
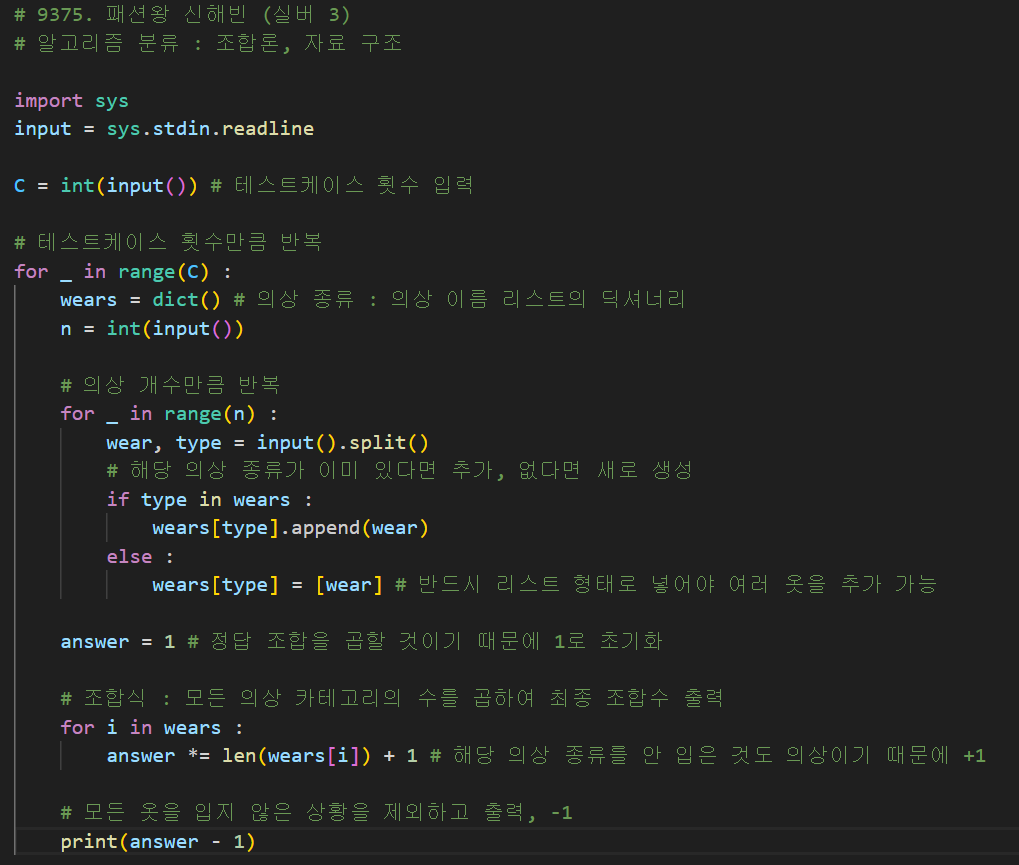
# 9375. 패션왕 신해빈 (실버 3)
# 알고리즘 분류 : 조합론, 자료 구조
import sys
input = sys.stdin.readline
C = int(input()) # 테스트케이스 횟수 입력
# 테스트케이스 횟수만큼 반복
for _ in range(C) :
wears = dict() # 의상 종류 : 의상 이름 리스트의 딕셔너리
n = int(input())
# 의상 개수만큼 반복
for _ in range(n) :
wear, type = input().split()
# 해당 의상 종류가 이미 있다면 추가, 없다면 새로 생성
if type in wears :
wears[type].append(wear)
else :
wears[type] = [wear] # 반드시 리스트 형태로 넣어야 여러 옷을 추가 가능
answer = 1 # 정답 조합을 곱할 것이기 때문에 1로 초기화
# 조합식 : 모든 의상 카테고리의 수를 곱하여 최종 조합수 출력
for i in wears :
answer *= len(wears[i]) + 1 # 해당 의상 종류를 안 입은 것도 의상이기 때문에 +1
# 모든 옷을 입지 않은 상황을 제외하고 출력, -1
print(answer - 1)
풀이 해설
우리는 보통 경우의 수를 생각할 때, 곱셈을 쓴다.
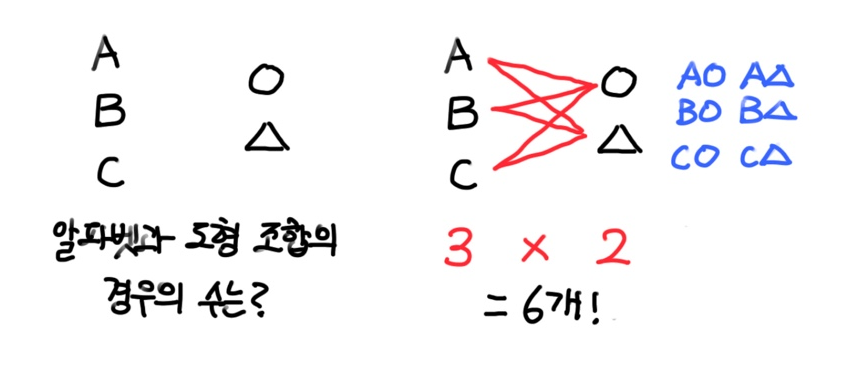
조합 역시 경우의 수와 매우 유사하다.
이 문제에서 만약 해빈이가 상의 3개와 하의 2개와 안경 3종류를 가지고 있다면,
해빈이의 의상 조합은 3 x 2 x 3 = 18개일 것이다.
그러나 이 문제는, 의상을 입지 않는다는 경우도 존재한다.
그럼 어떡하지? 3 x 2 x 3이 아닌, 안경을 쓰지 않은 3 x 2만 계산도 하고,
나머지도 전부 그렇게 처리해서 덧셈을 해야하나?
물론 그런 식의 수학적 접근도 가능하다.
의상의 종류를 하나만, 두개만, 세개 전부 입는다는 경우를 제각각 구하면,
3 + 2 + 3 + 3x2 + 3x3 + 2x3 + 3x2x3 = 47으로,
실제로 47은 정답이 맞다.
하지만 이렇게 복잡하게 수식을 만들 필요가 전혀 없다!
밑의 예시를 한번 봐보자.

해빈이가 상의 2개, 바지 3개를 가지고 있다고 할 때,
단순히 2 x 3으로는 우리가 원하는 답을 내지 못한다.
상의를 입지 않을 때도 있을 것이고, 하의를 입지 않을 때도 있을 거니까.

하지만 '안입는다' 라는 의상을 추가한다면?
복잡하게 어떤 카테고리의 의상은 계산하지 않고, 또 다음엔 계산하고... 할 필요 없이,
그냥 입지 않는다는 개념 또한 하나의 의상이라고 생각하면 순식간에 곱셈으로 접근이 가능해진다!
단, 주의해야 할 것은 '모든 옷을 입지 않는다'는 경우가 존재하게 되는 것이다.
문제에서 해빈이는 어떤 종류든 반드시 하나의 옷은 입는다는 전제가 있었으니,
모든 옷을 입지 않는다라는 경우 1을 제외하면 그것이 답이 된다.
만약 상술했던 가정인,
해빈이가 상의 3개와 하의 2개와 안경 3종류를 가지고 있다면,
각 카테고리에 입지 않는다라는 의상을 추가한 후 곱셈을 하면
4 x 3 x 4 = 48
여기서 아무것도 입지 않는다는 경우 1을 빼면
48 - 1 = 47
로 정답이 나오게 되는 것이다.
이런 접근법은 이후로도 조합론 문제를 풀 때 굉장히 도움이 된다.
눈에 보이는 것만 경우인 것이 아닌, 숨은 조건이 있다면 그 조건도 반드시 조합에 충족시키게끔 생각하는 것.
이것이 앞으로 만날 조합론 문제에서 핵심적인 수학적 접근법이 되겠다.
...와는 별개로, 이 문제는 의상의 종류가 매우 많고, 의상 자체도 많을 수 있으니
단순히 배열이나 리스트로 만들면 검색에 너무 많은 시간을 소요하게 될 것이다.
따라서, 의상 카테고리와 의상을 추가할 땐 반드시 해시를 사용하자.
파이썬에선 해시를 딕셔너리로 간단하게 구현 가능하다.
딕셔너리의 키를 의상 카테고리로, 값을 의상 이름으로 한다면, 검색이 훨씬 빨라질 것이다.
'문제 풀이' 카테고리의 다른 글
| [baekjoon] 1107. 리모컨 문제풀이 with Python (0) | 2023.03.30 |
|---|